栈
特点:
元素遵循先进后出的原则tt存储栈顶元素下标
定义
cpp
1 | int stk[N]; // 栈 |
插入
cpp
1 | stk[++ tt] = x; |
删除
cpp
1 | tt --; |
判空
cpp
1 | tt > 0 |
单调栈
分为单调递增栈和单调递减栈
含义:
栈中的元素是单调递增或单调递减的
对于栈中的 ax ay, ax 永远不会被作为答案输出,那么就在队列中删除 ax 以达到优化时间复杂度的目标
核心代码
cpp
1 | while (tt && stk[tt] >= tmp) tt --; |
单调栈:
求每一个数 左侧 / 右侧 离它最近且比他小的数,能将 O(n^2^) 的问题优化为 O(n)
cpp
1 | const int N= 1e5; |
队列
特点
元素前进先出,在队尾插入元素,在队头弹出元素
定义
cpp
1 | int q[N]; // 队列 |
插入
cpp
1 | q[++ tt] = x; |
弹出
cpp
1 | hh ++; |
队列判空
cpp
1 | hh <= tt |
循环队列
单调队列 / 滑动窗口
能够将 O(n^2^) 的时间复杂度优化成 O(n)
例题
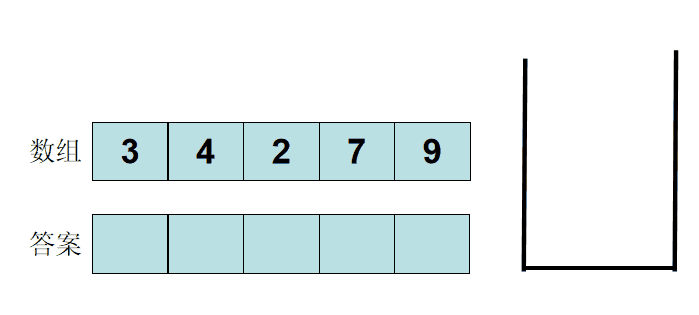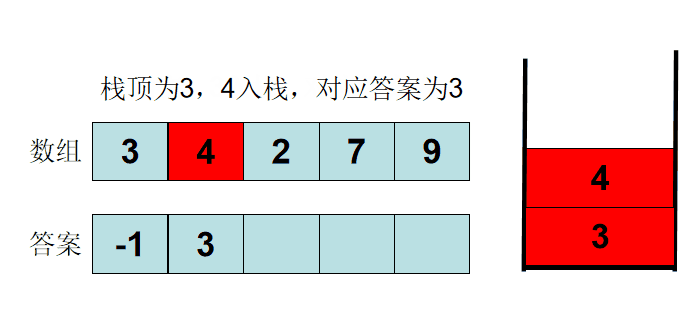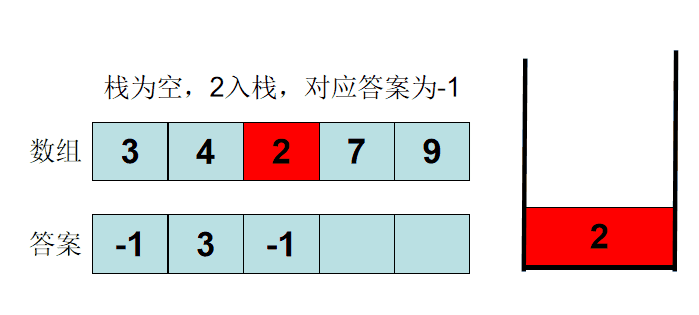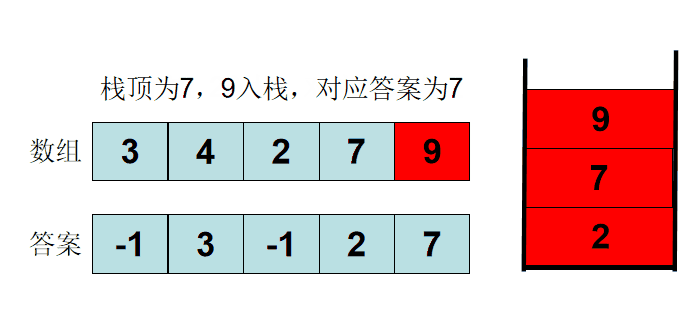
cpp
1 | const int N = 1e6; |



